Que es numero : 2015

miércoles, 25 de febrero de 2015

1.- La ley de gravitación de Newton establece que la fuerza de atracción entre dos cuerpos es directamente proporcional al cuadrado de la distancia que los separa. Si una masa aumenta un 15% y la distancia entre las masas disminuye 15%, calcular el porcentaje de cambio en la otra masa para que la fuerza de atracción tenga un aumento de un 15%.

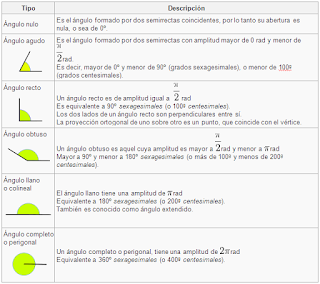
52. en cada uno de los siguientes casos transforma el ángulo expresado en radianes a grados:

(a) 0.5 rad= 28.66º
(b) 0.75 rad= 42.99º
(c) 1rad= 57.32º
(d) 1.25 rad= 71.65º
(e) 1.5 rad= 85.98º
(f) 2 rad= 114.64º
(g) 2.5 rad= 143.31º
(h) 3 rad= 171.97º

En cada uno de los siguientes casos transforma el ´angulo expresado en grados a radianes:

(a) 10◦= 0.174 rad
(b) 15◦= 0.261 rad
(c) 30◦= 0.523 rad
(d) 45◦= 0.785 rad
(e) 60◦= 1.047 rad
(f) 75◦= 1.308 rad
(g) 90◦= 1.57 rad
(h) 180◦= 3.14 rad

Traza un pentágono regular y usando la notación convenido señala los siguientes elementos

apotema, lado, radio, diagonal, vértice y ángulo interno.

¿Como se clasifican los polígonos según la longitud de sus lados?

a) Regulares los lados miden lo mismo

.
b) Irregulares la longitud de lados es distinta.

¿Como se clasifican los polígonos según el tipo de ángulos?

Como se clasifican los polígonos según el numero de lados que tiene?

Triángulo, cuadrilátero, Pentágono, hexágono, heptágono, octágono, eneagono, decágono, endecágono, dodecágono, chiliagono (1000), etc

¿Que es una línea quebrada?

Segmentos de recta que no están sobre una misma recta
.

En cada uno de los siguientes casos calcula la longitud del arco:

(a) r= 2 y α = 30◦ = 1.04
(b) r= 4 y α = 60◦ = 4.18
(c) r= 1.2 y α = 38◦ = 0.79
(d) r= 32 y α = 45◦ = 25.12
(e) r= 5 y α = 98◦ = 8.54
(f) r= 7 y α = 120◦ = 14.65
(g) r= 11y α = 270◦ = 51.81

Traza una circunferencia y usando la notación correcta señala los siguientes elementos: radio, diámetro, cuerda, secante, segmento circular, sector circular.

¿Como se denota una semi-recta?

Resultado de imagen para semi recta denotacion

Cómo se denota una recta? Recta AB

¿Qué es una linea recta?

Las rectas no tienen comienzo ni final: son líneas compuestas de puntos que se suceden de manera indefinida. Están consideradas como uno de los entes fundamentales de la geometría, al igual que los ya mencionados puntos y los planos.

Es una línea que toca dos veces el plano y es infinita

¿Que es un plano?

Es una superficie plana de dimensión 2

Es un objeto ideal que solo posee dos dimensiones, y contiene infinitos puntos y rectas; es un concepto fundamental de la geometría junto con el punto y la recta.

Cuando se habla de un plano, se está hablando del objeto geométrico que no posee volumen, es decir bidimensional, y que contiene un número infinito de rectas y puntos. Sin embargo, cuando el término se utiliza en plural, se está hablando de aquel material que es elaborado como una representación gráfica de superficies en diferentes posiciones

¿Que es un punto?

Es lo que separa las lineas adyacentes

El punto en geometría es un ente fundamental: esto quiere decir que sólo puede definirse realizando una comparación con otros elementos. De este modo, el punto no se define por sí mismo, sino que adquiere su significado a partir de su relación con otros conceptos

¿Que es una línea?

Es lo que supera superficies adyacentes

Sucesión continua de puntos en el espacio.

Señal o marca larga y estrecha que se hace o se forma sobre un cuerpo o superficie.

¿Qué es una superficie?

Es lo que separa a un objeto geométrico del resto del espacio.

Una superficie es de hecho un conjunto de puntos de un espacio euclídeo que forma un espacio topológico bidimensional que localmente, es decir, visto de cerca se parece al espacio euclídeo bidimensional. Así alrededor de cada punto de una superficie esta se aproxima bien por el plano tangente a la superficie en dicho punto.

¿Que es un solido geométrico?

Un Sólido CuerpoGeométrico es una figura geométrica de tres dimensiones (largo, ancho y alto), que ocupa un lugar en el espacio y en consecuencia tiene un volumen.

Traza con regla y compás las siguientes figuras geométricas (a) Una perpendicular a un segmento dado.

(a) Una perpendicular a un segmento dado
(b) Un angulo de 60◦
(c) Un angulo de 30◦
(d) Un angulo de 45◦
(e) Una línea paralela a una recta dada.
(f) Un triángulo de 3, 4 y 5 cm.

(g) Un hexágono de lado 4cm.

(h) Un cuadrado de lado 5 cm.

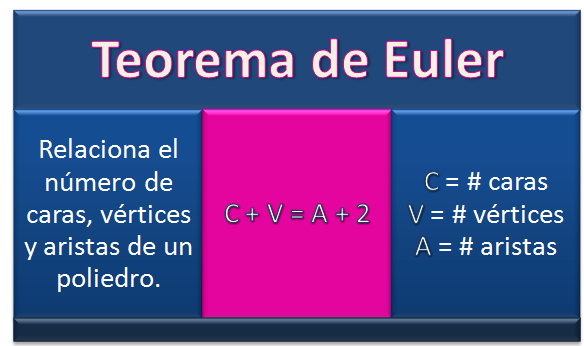
Escribe tres ejemplos de teoremas matemáticos?

Primer sistema de tales, Teorema de pitagoras, Teorema de Euler.

¿Qué es un teorema?

La palabra teorema consiste en una proposición que puede ser demostrada de manera lógica a partir de un axioma o de otros teoremas que fueron demostrados con anticipación. Este proceso de demostración se lleva a cabo mediante ciertas reglas de inferencia.

Afirmación que se hace dentro de un sistema lógico y que puede ser demostrado a partir de los axiomas.

Escribe tres ejemplos de postulados matemáticos?

1. - Una recta puede trazarse desde un punto cualquiera hasta otro.

2. - Una recta finita puede prolongarse continuamente y hacerse una recta ilimitada o indefinida.

3. - Una circunferencia puede describirse con un centro y una distancia.

4. - Todos los ángulos rectos son iguales entre sí.

5. - Si una recta que corte a otras dos forma con éstas ángulos interiores del mismo lado de ella que sumados sean menores que dos rectos, las dos rectas, si se prolongan indefinidamente, se cortan del lado en que dicha suma de ángulos sea menor que dos rectos.

¿Qué es un postulado?

Proposición no evidente por si misma, ni demostrada pero que se acepta que no existe otro principio del que pueda ser deducida

Proposición que se toma como base para un razonamiento o demostración cuya verdad se admite sin pruebas.

Escribe tres ejemplos de axiomas matemáticos.

Si a cantidades iguales se les añaden cantidades iguales, las sumas resultantes también son iguales
El todo es mayor que cualquiera de sus partes
Dos puntos determinan una recta y solamente una a la que pertenecen.
La probabilidad de un suceso esta entre 0 y 1
X=X

¿Qué es un axioma?

Verdades incuestionables universalmente válidas y evidentes, que se utilizan a menudo como principios en la construcción de una teoría o como base para una argumentación.
Proposición que se considera evidente y se acepta sin requerir demostración previa

¿Para qué sirve la lógica?

Resultado de imagen para logica para que sirve

¿Para que sirve la lógica?

La lógica sirve para explicar fenómenos de la vida cotidiana, basándose en la razón como principal interviniente en este proceso; el pensar lógicamente ayuda a el hombre a interrogarse por el funcionamiento de todo lo que nos rodea, la lógica sirve para argumentar y es de cierta manera un pensamiento o una idea que nos fluye poruna acción que realizamos en nuestra vida diaria.

Escribe 5 ejemplos donde se muestre la falacia de la afirmación del consecuente

a) Todo alumno de bachillerato carece de titulo. José carece de titulo profesional. José no tiene titulo profesional por lo tanto no esta en bachillerato.
b) Todo niño es juguetón. Benito es juguetón. Benito es un niño.
c) Todo automóvil tiene ruedas. El aeroplano tiene ruedas. El aeroplano es un automóvil.
d) Todo paralelogramo es cuadrilátero. El trapecio es un cuadrilátero. El trapecio es un paralelogramo.
d) Ningún ave tiene dientes. El oso hormiguero no tiene dientes. El oso hormiguero no es un ave.

Resultado de imagen para bachillerato

¿En qué consiste la falacia de la afirmación del consecuente?

Se produce cuando en un argumento condicional se concluye afirmando el consecuente. Por ejemplo:

Si alguien es merengue, entonces le va al Real Madrid
El Cid es merengue.
Luego, le val .
En esquema:
Si C, entonces D.
B es D
Luego, B es C.
Olvida esta falacia que B puede ser consecuencia de otras cosas distintas de C.
Si alguien toma cianuro se morirá.
La abuela se ha muerto,
Luego, ha tomado cianuro.
El consecuente forma una condición necesaria. Si falta (si la negamos) podemos negar el antecedente: Si no se ha muerto es seguro que no ha tomado cianuro. Por el contrario, si la afirmamos, no podemos extraer ninguna conclusión porque no es una condición suficiente: puede haber muerto de otras muchas maneras.

Analiza las siguientes premisas y escribe la conclusión que deduzcas:

(a) todos los hombres son imperfectos y el maestro de matemáticas es hombre, entonces... el maestro de matemáticas es imperfecto.

(b) Los planetas carecen de luz propia. Venus es un planeta. Por lo tanto,Venus carece de luz propia.

(c) Si todos los X son Y y todos los Z son X, entonces.. todos los Y son Z.
.
(d) Todos los hombres son mortales. Un dictador es un hombre. Por lo tanto, Por lo tanto, el dictador es mortal

(e) Ningún cuadrilátero es triángulo. El rombo es un cuadrilátero. Por lo tanto, el rombo no es un triángulo.

(f) Si todos los elementos de A pertenecen a B y todo elemento de B es un elemento de C, entonces... B y C pertenecen a A.

martes, 24 de febrero de 2015

¿En que consiste el silogismo llamado modus tollens?

La tautología conocida como Modus Tollens adquiere la siguiente forma de ley lógica:

[(p

¬q]

¬p

que, traducido al lenguaje natural sería algo así como si p implica q, y q es falso, entonces p también debe ser falso.

Sea p:"hago mucho deporte", y q:"estoy cansado", según este esquema tautológico:

"Si hago mucho deporte, entonces estoy cansado, y no es cierto que estoy cansado, por lo que no hago mucho deporte

¿En que consiste el silogismo llamado modus ponens?

Es una forma simple de argumento valido y regla de inferencia . Se puede resumir como "P entonces Q; P se afirma siendo verdad, por lo que, por tanto, Q debe ser verdad." La historia del modus ponens se remonta a la antigüedad.

\frac{P \to Q,\; P}{\therefore Q}

Que es numero